삼각형의 면적 구하기 (Heron's formula)

Heron's formula에 의하면 삼각형 ABC의 넓이는 다음과 같다. 단, s는 (a+b+c)/2로 정의한다.

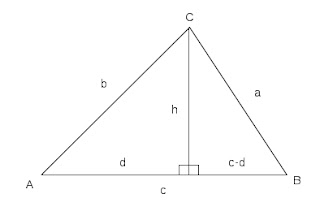
위와 같은 식은 다음과 같이 유도할 수 있다.

삼각형 ABC를 수직으로 분할하는 두 개의 삼각형에 대한 피타고라스의 정리는 다음과 같은 관계식을 제공한다.

그리고 두 수식으로부터 다음과 같은 관계식을 유도할 수 있다.

그럼 삼각형 ABC의 넓이는 c*h/2이고 이 넓이의 제곱값은 다음과 같이 전개할 수 있다.

그리고 s=(a+b+c)/2로 정의하면 Heron's의 방정식은 증명된다.


/* By Heron's formula, the area of the triangle
   sqrt(s*(s-a)*(s-b)*(s-c)), s: (a+b+c)/2 */
real_t triangle_area(triangle_t *tri)
{
  real_t s, a, b, c;

  assert(tri);

  a = distance_between_points(tri->b, tri->c);
  b = distance_between_points(tri->c, tri->a);
  c = distance_between_points(tri->a, tri->b);
  s = (a + b + c) / 2;

  return sqrt(s * (s - a) * (s - b) * (s - c))
}